
|
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|

| 9-11 классы |
 |
1. В каждой клетке шахматной доски стоит оловянный солдатик. Все 64 солдатика разной величины. Среди каждых восьми солдатиков, составляющих горизонтальный ряд, выбирают самого большого. После этого из отобранных восьми больших солдатиков выбирают самого маленького. Затем среди каждых восьми солдатиков, составляющих вертикальный ряд, выбирают самого маленького. После этого из отобранных восьми маленьких солдатиков выбирают самого большого. Какой солдатик больше: самый маленький из больших или самый большой из маленьких? |
 |
2. В Стране Чудес проводилось следствие по делу об украденном бульоне. На суде Мартовский Заяц заявил, что бульон украл Болванщик. Соня и Болванщик тоже дали показания, но что они сказали, никто не запомнил, а запись смыло алисиными слезами. В ходе судебного заседания выяснилось, что бульон украл лишь один из подсудимых и что только он дал правдивые показания. Так кто украл бульон? |
 |
3. Путешественник выходит из гостиницы в 3 часа дня и возвращается в 9 часов вечера, по тому же маршруту. Известно, что по ровным участкам он идет со скоростью 4 км/ч, в гору – 3 км/ч, под гору – 5 км/ч. Найдите расстояние, которое прошел путешественник, если он шел без отдыха. |
 |
4. Эта старинная задача была известна ещё в Древнем Риме. Богатый сенатор, умирая, оставил жену в ожидании ребёнка. После смерти сенатора выяснилось, что на своё имущество, равное 210 талантам, он составил следующее завещание: «В случае рождения сына отдать мальчику две трети состояния (т. е. 140 талантов), а остальную треть (т. е. 70 талантов) — матери; в случае же рождения дочери отдать девочке одну треть состояния (т. е. 70 талантов), а остальные две трети (т. е. 140 талантов) — матери». У вдовы сенатора родились близнецы — мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наилучшим приближением к условию завещания? |
 |
5. Круглый бассейн, диаметром 6 м, до краев наполнен водой. В центре бассейна растет тростник, верхушка которого возвышается над поверхностью воды на 1 м. Если притянуть тростник к берегу, его верхушка коснется края бассейна. Определить глубину бассейна. |
 |
6. Учёный с мировым именем Иннокентий решил плотно пообедать и с аппетитом съел комплексный обед из трёх блюд. Масса первого блюда — 550 граммов, объём — 0,0005 м³. Масса второго — 150 граммов, объем — 0,0002 м³. Масса компота — 1 кг 100 граммов, объём — 0,0011 м³. Как вычислить среднюю плотность плотного обеда, который учёный с мировым именем съел без хлеба? |
 |
7. Подарочный набор состоит из трех сортов конфет. Массы конфет первого, второго и третьего сортов в этом наборе относятся как 3 : 7 : 10. Массу конфет первого сорта увеличили на 8%, а второго – на 4%. На сколько процентов надо уменьшить массу конфет третьего сорта, чтобы масса всего набора не изменилась. |
 |
8. Дед, взявшись за репку, развивает силу тяги до 600 Н, бабка до 100 Н, внучка до 50 Н, Жучка до 30 Н, кошка до 10 Н и мышка до 2 Н. Чему равна равнодействующая всех этих сил, направленных по одной прямой в одну и ту же сторону? Справилась бы с репкой эта компания без мышки, если силы, удерживающие репку в земле, равны 791 Н? |
 |
9. Вот семь венгерских существительных: nyírfa, körte, alma, almak, körtefa, nyírfak, almafa. А вот их переводы на русский язык: берёза, груша, яблоня, яблоко, берёзы, яблоки. (Заметьте: этими шестью русскими словами переведены все семь венгерских!) Установите, какое венгерское слово, какому русскому соответствует. |
 |
10. У крестьянина есть 6 кусков цепи по 5 звеньев в каждом, из которых он хочет сделать одну длинную и замкнутую цепь, состоящую из 30 звеньев. Разрезать одно звено стоит 8 копеек, а вновь соединить его — 18 копеек. Однако можно просто купить новую замкнутую цепь из 30 звеньев за полтора рубля. Каким образом возможно изготовить цепь из имеющихся б кусков и сколько денег при этом можно сэкономить? |
 |
11. На дне озера бьют ключи. Стадо из 183 слонов могло бы выпить озеро за один день, а стадо из 37 слонов - за 5 дней. За сколько дней выпьет озеро один слон? |
 |
12. (Задача И. Ньютона) 70 коров съели бы траву на лугу за 24 дня, а 30 коров - за 60 дней. Сколько коров съели бы траву за 96 дней? |
 |
13. На каком из рисунков закрашена большая площадь? (Сторона каждого квадрата делится на 3 равные части.) |
 |
14. Четыре одинаковые игральные кости уложены так, как показано на рисунке. Сколько точек на самой нижней грани? |
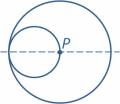 |
15. Окружность радиуса 1 катится без скольжения по окружности радиуса 2 с внутренней стороны. На меньшей окружности отмечена точка Р, которая в начальном положении совпадает с центром большей окружности. Какова траектория точки Р? |
 |
16. Каково отношение площади закрашенной части к площади белой части? |
| 1 2 3 4 5 6 7 8 9 10 11 |
|
|

|
| « Март 2026 » | | Пн | Вт | Ср | Чт | Пт | Сб | Вс | | | | | | | | 1 | | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | 16 | 17 | 18 | 19 | 20 | 21 | 22 | | 23 | 24 | 25 | 26 | 27 | 28 | 29 | | 30 | 31 |
|
|

























